近日,中国科学技术大学国际金融研究院高水平理论研究取得新突破,特任副教授何欣合作论文“Growing the Efficient Frontier on Panel Trees”发表于金融学三大顶刊之一《Journal of Financial Economics》。这是中国科学技术大学在金融学三大顶刊发表的首篇论文,是中国科学技术大学管理学院、科技商学院、国际金融研究院融合发展的重要成果。

何欣 中国科学技术大学特任副教授
教师主页:https://bs.ustc.edu.cn/chinese/profile-2437.html
近年来,中国科学技术大学国际金融研究院专注金融领域,开展高水平前沿研究、推动金融创新落地。这篇论文的发表为中国科学技术大学国际金融研究院下一步高质量发展开启了良好局面,将助力其在金融领域持续攀登新高峰。未来,中国科学技术大学国际金融研究院将搭建更加广阔的学术资源共享平台,吸引全球金融领域的顶尖人才汇聚,为基础创新注入源源不断的智力支持。

研究背景
随着生成式大语言模型兴起,2024年诺贝尔奖的公布也彰显了神经网络和人工智能领域的研究成果。虽然金融学者们也在尝试采用“大模型”的思路,但透明、可解释且易于运算的模型仍然是科学技术工作者的首选。DeepSeek横空出世指出:优良的算法比堆砌算力更加重要。金融领域的人工智能应用是否只能局限于大模型和生成式语言模型的范畴?
康奈尔大学的Lin William Cong,香港城市大学的冯冠豪和何靖宇,和中国科学技术大学的何欣的引领性工作“Growing the Efficient Frontier on Panel Trees”,提出了一种新颖的面板树模型。该模型不仅体现了《孙子兵法》中“分而治之”的智慧,也有效应对了高维大数据带来的挑战。面板树模型虽然借鉴了人工智能中扩大模型空间以目标导向搜索解决方案的思想,但它不依赖于深度学习或强化学习,成为了金融应用中一个既透明又高效的“小而美”模型。这项合作成果是金融学顶级期刊《Journal of Financial Economics》近期首次接收非文本、非深度学习的人工智能研究文章,不仅获得了金融投资界的广泛关注,还荣获了2022 INQUIRE Europe Research Grant Award和2024 IQAM Research Prize等多项荣誉。该论文的P-Tree测试资产和因子数据公开在网址:https://quantactix.github.io/P-Tree-Public-Data/,欢迎下载和引用。
作者简介(按姓氏首字母排序)
 丛林 康奈尔大学
丛林 康奈尔大学  冯冠豪 香港城市大学
冯冠豪 香港城市大学
 何靖宇 香港城市大学
何靖宇 香港城市大学  何欣 中国科学技术大学
何欣 中国科学技术大学
摘 要
We introduce a new class of tree-based models, P-Trees, for analyzing (unbalanced) panel of individual asset returns, generalizing high-dimensional sorting with economic guidance and interpretability. Under the mean-variance efficient framework, P-Trees construct test assets that significantly advance the efficient frontier compared to commonly used test assets, with alphas unexplained by benchmark pricing models. P-Tree tangency portfolios also constitute traded factors, recovering the pricing kernel and outperforming popular observable and latent factor models for investments and cross-sectional pricing. Finally, P-Trees capture the complexity of asset returns with sparsity, achieving out-of-sample Sharpe ratios close to those attained only by over-parameterized large models.
本文介绍了一种创新的决策树模型——面板树(Panel Trees,简称P-Trees),旨在分析非平衡的个股面板数据。P-Trees模型扩展了金融学中高维排序分组问题的关键领域,致力于构建既具有经济学意义又可解释的有效测试资产。在均值-方差投资理论的框架下,P-Trees生成的测试资产显著扩展了投资的有效前沿,超越了文献中常用的测试资产。此外,P-Trees生成的因子不仅能够解释横截面上收益率的波动,还可直接应用于投资,展现出稳健的样本外性能。研究还表明,尽管P-Trees模型适用于从小规模到超大规模的多种情景,但即使是小规模的P-Trees模型也足以捕捉股票收益率的复杂性,其样本外夏普比率接近于超大规模模型的水平。
1 面板树模型
1.1 传统的树模型
图1展示了传统树模型CART如何利用股票特征来预测股票收益率。CART通过递归地将特征空间划分为更细分的子集,例如小盘股、大盘成长股和大盘价值股等,来实现这一目标。在树结构的底部,我们可以看到叶节点,CART模型采用同一叶节点内资产收益率的平均值作为该节点的预测值。

然而,传统的树模型并不完全适用于经济金融领域中常见的面板数据,也无法有效生成测试资产或资产定价因子。这些模型存在以下主要局限性:
1.独立同分布的假设:传统树模型将资产收益率的面板数据视为独立同分布(i.i.d.),这忽略了面板数据中的时间序列和横截面相关性。
2.局部划分准则:传统模型依赖于统计上的局部划分准则进行预测,例如使用子节点内的误差平方和作为目标函数。这种方法无法考虑面板数据的特性和经济学理论。
随着树的不断生长,每个节点中的观测值数量减少,这不仅增加了噪声,也不可避免地导致了过拟合问题。虽然树的集成学习方法(Ensemble Learning)可以在一定程度上缓解过拟合,但集成模型的可解释性不如单个决策树,且难以进行有效的可视化。
1.2 面板树及其创新
P-Tree通过以下方式解决了这两个问题:(1)假设树结构不随时间改变;(2)考虑横截面上所有观测值作为划分准则来引导树的生长,而不仅仅是某一个节点中的观测值。P-Tree既能充分提取面板数据来构建叶节点的测试资产,也能缓解过拟合,并将树的应用范围从纯预测领域扩展到生成测试资产和因子的目标导向聚类领域(Goal-Oriented Cluster)。
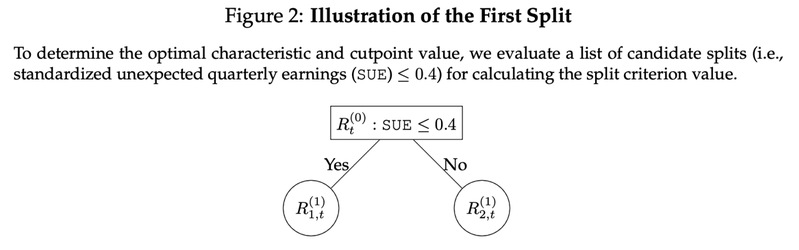
P-Tree模型的第一步是选出一个特征和一个分位数构成,作为第一次划分横截面的准则(Split Criteria)。例如,图2示意了一个备选的划分准则:按照股票的SUE在40%分位数进行划分,得到左边的叶子节点代表低SUE的资产组合,右边的叶子节点代表高SUE的资产组合。
P-Tree生成的因子是一组测试资产构成的均值-方差有效投资组合(Mean Variance Efficient Portfolio)。P-Tree的划分准则是最大化因子的夏普比率(Sharpe Ratio),如下列公式所示。经过搜索一系列潜在的股票特征和分位数,我们可以得到很多个可能的因子,从中我们选出夏普比率最高的一组股票特征和分位数作为第一次划分的决定。
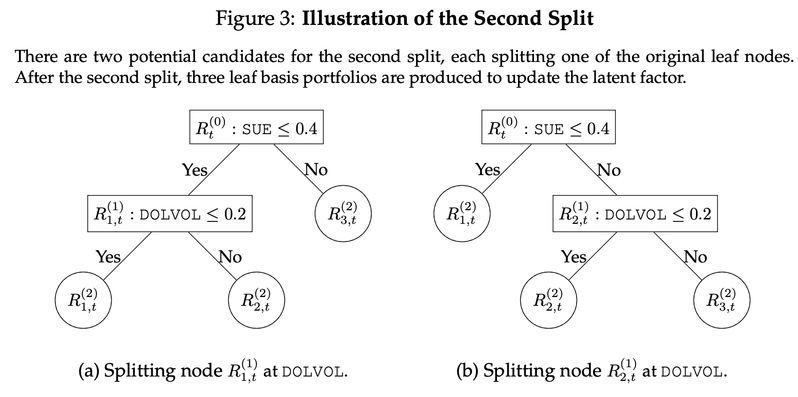
第二步,我们可以选择从左边的叶子节点划分,也可以选择从右边的叶子节点划分。如图三所示,在第二次划分后,我们得到三个叶子节点,用于构建因子并计算其夏普比率。类似第一步的方法,我们搜索一系列潜在的股票特征和分位数,并从中选出夏普比率最高的一组被划分的叶子节点、股票特征、分位数作为第二次划分的决定。
后续的划分决定类似于第二步的方法,我们可以将P-Tree不断向下生长,这也意味着横截面被划分得越来越精细。P-Tree有很多参数可以选择来进行模型的正则化,例如:树的层数,叶子的数量,最小的叶子包含的股票数量,等等。在本文的实证研究中,P-Tree在产生10个叶子后就停止生长,这样的小模型可以帮助我们可视化树的结构。
P-Tree还有很多可以拓展到集成学习,这里举两个例子。(1)与boosting结合,可以产生多个P-Tree,这类似金融学中的多因子模型。(2)与random forest结合,可以产生random P-Forest,应用到样本外预测和投资。
2 实证研究
2.1数据和实验设计
在实证分析部分,作者采用了1981年至2020年,总计40年的美国市场股票月度数据作为研究样本。这一时间段的选取为模型提供了长期且全面的市场信息,使其结果更具代表性和说服力。样本涵盖了60个不同的特征,这些特征被归类为六个主要类别,包括动量、价值、投资、盈利能力、市场摩擦(例如规模)以及无形资产。为了进一步验证模型的稳健性,作者采用了前20年的数据作为训练集,来构建和优化模型,而后20年的数据则作为测试集,用于评估模型的样本外预测能力和投资性能。
2.2 用面板树来划分股票的横截面
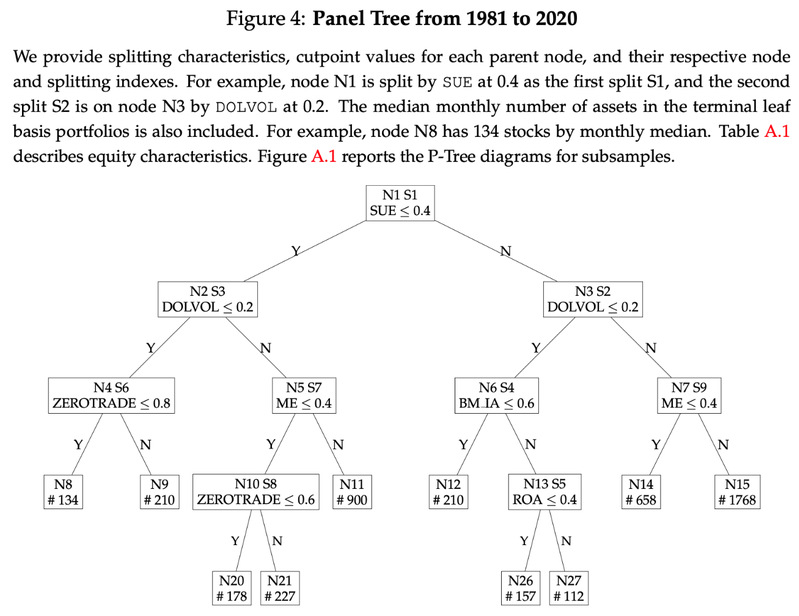
相较于深度学习和大语言模型,面板树的一大优势是她非常适合可视化。文中的图4展示了面板树的结构。其中,模型既选取基本面相关股票特征,例如SUE和BM,也兼顾了技术面的股票特征,例如DOLVOL,ME等。P-Tree对横截面的划分由数据驱动,非常灵活,突破了传统的低维度、对称划分的排序分组方法。
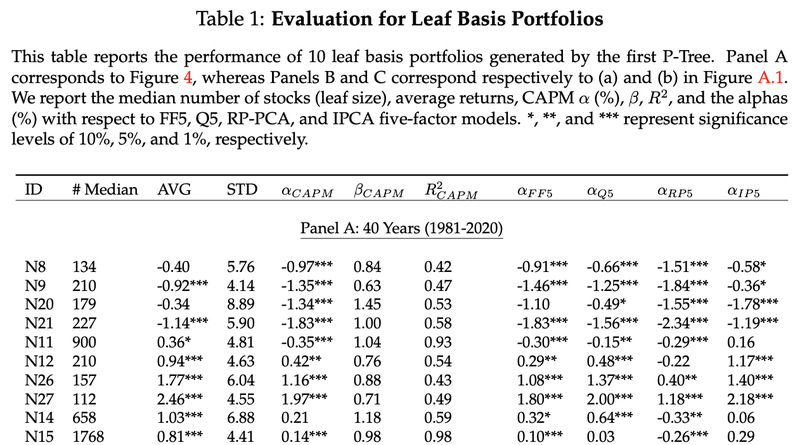
2.3 测试资产
表1展示了由P-Tree模型生成的测试资产的各项特性,包括股票数量、预期收益率、波动性、Alpha和Beta等统计指标。分析结果表明,在10个由P-Tree生成的测试资产中,有9个展现出了显著的CAPM Alpha值。即使在应用其他因子模型(如FF5、Q5、RPPCA5和IPCA5)进行测试时,这些P-Tree生成的测试资产仍然显示出显著的Alpha。这表明现有的因子模型难以完全解释这些测试资产的表现。
这些测试资产的显著Alpha值说明着它们有潜力推动投资组合有效前沿的拓展,从而实现更高的风险调整后收益。这一发现表明,P-Tree模型不仅能够生成具有经济意义的测试资产,还能揭示出传统因子模型未能捕捉到的投资机会。因此,这些测试资产对于寻求提高投资效率和探索新因子模型的投资者和研究人员而言,具有重要的价值。
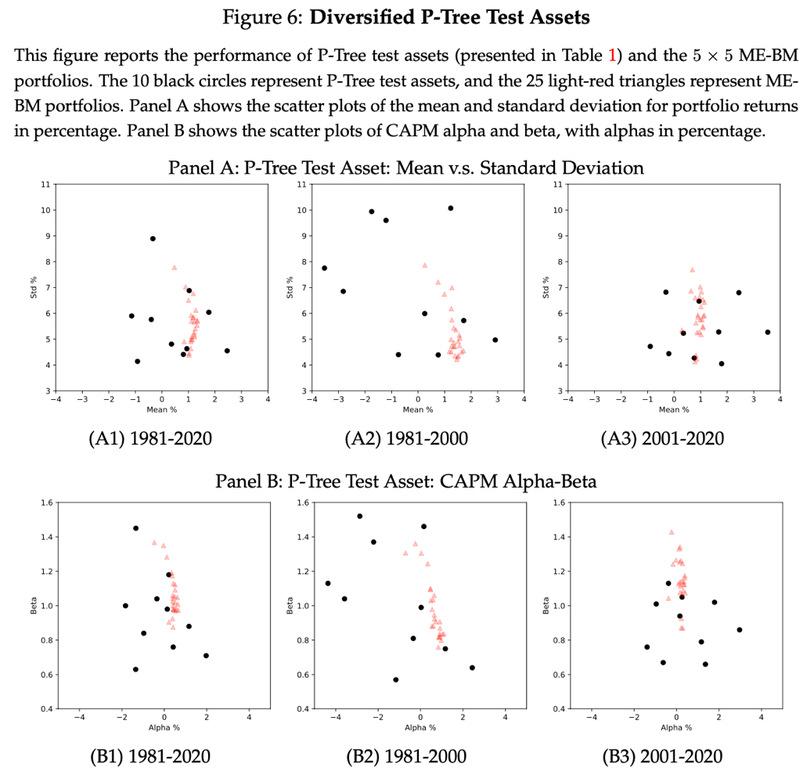
在投资界,不把所有鸡蛋放在一个篮子里的格言广为流传,它强调了分散投资以降低风险的智慧。图6的A板块生动地展现了P-Tree测试资产的分散化特征。特别地,子图A1基于1981至2020年的40年数据,以黑圈形式描绘了首个P-Tree的叶节点测试资产的收益与风险(标准差)的散点图。这些资产在预期收益和风险上呈现出的明显差异,验证了它们在均值-方差有效前沿(MVE)框架内的分散化优势。相形之下,以浅红三角表示的5×5市值-账面市值比(ME-BM)组合则围绕一个平均收益水平聚集,显示出较低的分散化程度。这一对比揭示了P-Tree测试资产在MVE框架下具有更优的分散化特性。
图6的B板块进一步揭示了资本资产定价模型(CAPM)下的Alpha-Beta关系。在子图B1中,P-Tree测试资产的CAPM Beta值分布在0.6到1.6的区间,而CAPM Alpha值则接近零,介于-2%到2%之间,反映了这些资产在CAPM框架下的波动性。尽管如此,5×5 ME-BM组合的CAPM Alpha值更接近于零,且更紧密地围绕零Alpha线分布,表明它们在CAPM模型下的解释力更强,且在所有图表中表现出较低的分散度。总体来看,P-Tree测试资产在CAPM定价下仍展现出比传统ME-BM组合更优的分散化模式。
2.4 有效前沿
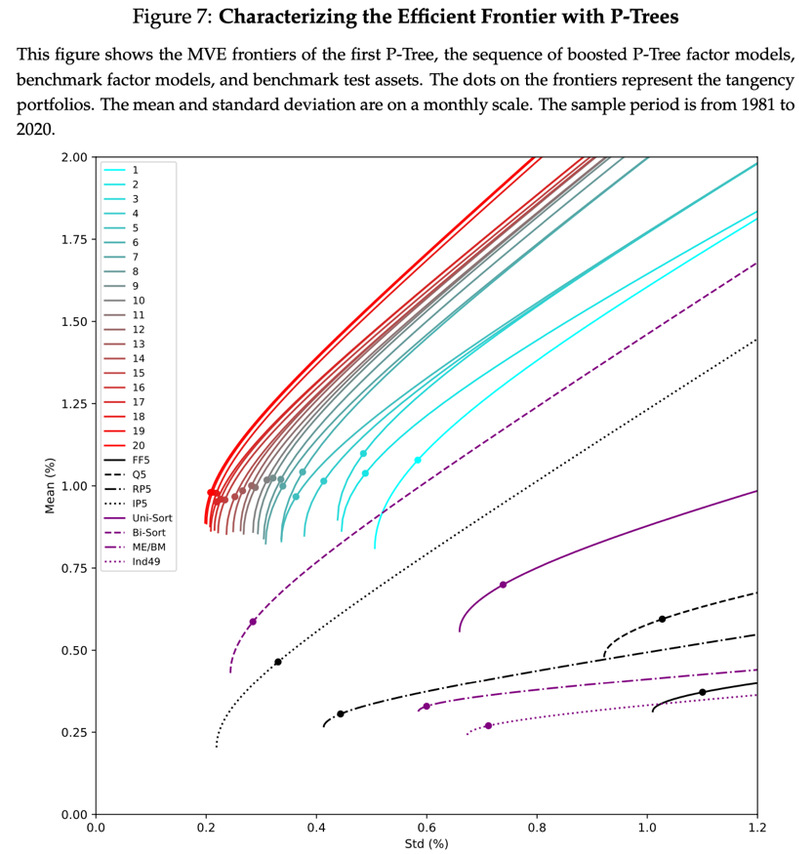
图7描绘了1981年至2020年样本期间P-Tree及其增强版本Boosted P-Tree的均值-方差有效前沿。这些有效前沿以从蓝色到红色的渐变色调呈现,形象地展示了风险与收益之间的权衡。作为参照,传统的因子模型有效前沿以黑色表示,而作为对比的测试资产则以紫色标示。分析结果揭示,由首个P-Tree生成的10个测试资产构成的有效前沿,在效率上超越了所有基于标准因子模型和对比测试资产构建的有效前沿。
在所有比较基准中,尽管基于双变量排序的285个投资组合构建的有效前沿与我们的第一个P-Tree前沿相当接近,但P-Tree仅使用了10个投资组合,远少于285个。此外,即便在因子模型中表现突出的IPCA五因子模型,其有效前沿仍然未能超越第一个P-Tree的前沿。总体来看,第一个P-Tree创造了10个独特的测试资产,形成了一个效率极高的有效前沿。相比之下,传统的基准因子模型和测试资产并未能构建出真正高效的投资前沿。
通过Boosting这一集成学习方法的辅助,我们能够生成多个P-Tree,从而持续推动有效前沿的边界向外扩展。如图所示,随着使用的因子数量增加,有效前沿不断向左上角延伸,这表明在相同风险水平下,投资者能够实现更高的收益。这一发现强调了P-Tree及其增强版本在金融投资领域的巨大潜力,为投资者提供了更为丰富和高效的投资策略选择。
3 结 论
本文的研究结果证实,P-Tree模型在资产定价领域生成的测试资产展现出了明显的优越性,特别是在处理高维特征、交互项和非线性关系这些挑战时表现得尤为出色。与那些传统的排序和分组方法及其产生的测试资产相比,P-Tree在划分资产横截面时展现出更大的灵活性,并且能够生成更为有效的测试资产,适用于实证资产定价的多种应用场景。相较于那些结构复杂的深度学习和大型模型,P-Tree模型以透明且规模适中的特性脱颖而出,并在样本外测试中表现出色。
文章不仅为金融学中传统的排序和分组方法提供了创新的替代选择,还展示了人工智能技术在金融数据建模中的广泛应用潜力。此外,研究强调了经济学理论在金融大数据分析和大型模型构建中的核心作用,并为资产定价领域的未来研究指明了新的方向,推动了该领域研究方法的创新和发展。
原文链接:https://doi.org/10.1016/j.jfineco.2025.104024
